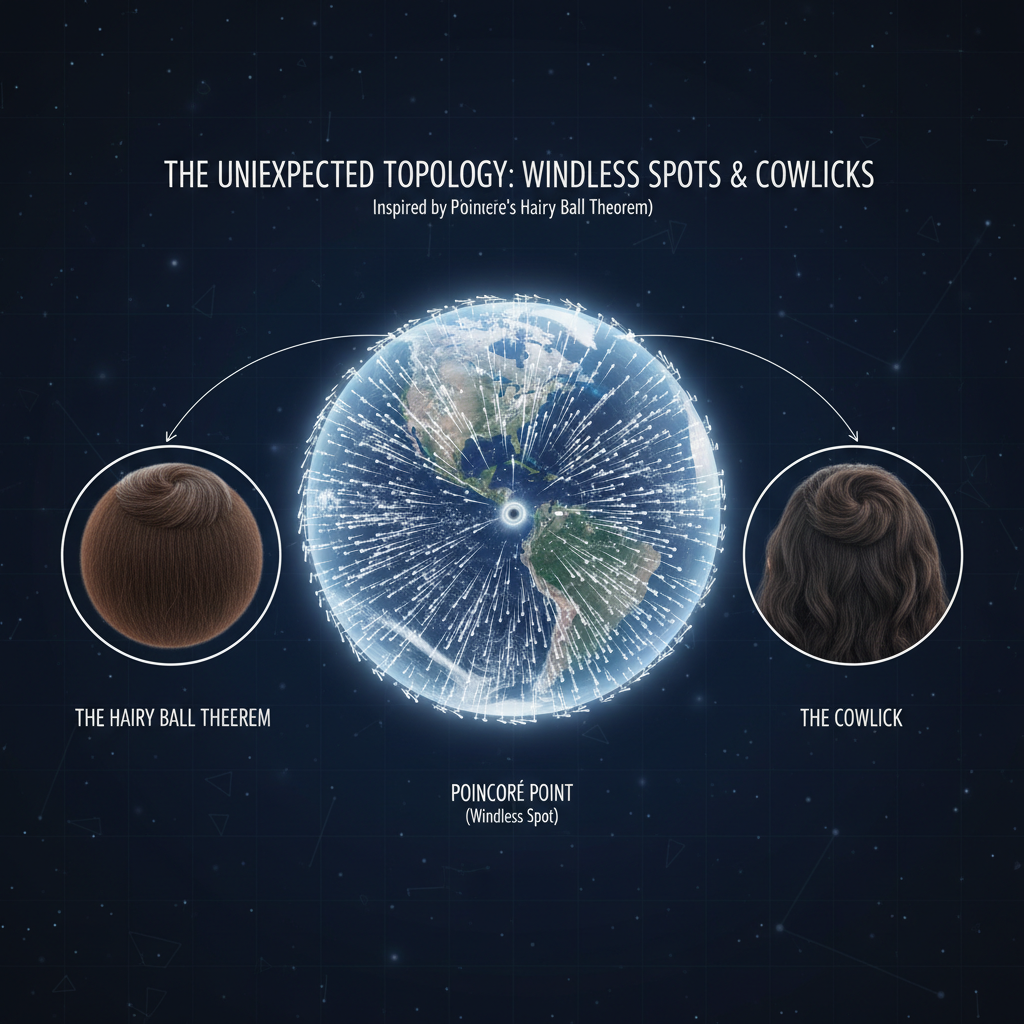
あなたの知らない地球の秘密
天気予報を毎日チェックしているあなたも、おそらく一度は「風速0m/s」という表示を見たことがあるでしょう。それは特定の地域、特定の瞬間の穏やかな気象状況を示しています。しかし、もしこう言われたらどうでしょう?
「地球上のどこかでは、この瞬間も、そしていかなる瞬間も、必ず風が完全に止まっている『無風地点』が存在する」
これは偶然ではありません。嵐がどれだけ吹き荒れようと、ジェット気流がどれだけ強く流れようと、地球という球体の上には、数学的に「存在せざるを得ない」静寂の場所があるのです。
「そんな馬鹿な話があるか」と思うかもしれません。しかし、この驚くべき事実は、今から130年以上も前の1885年に、一人の天才数学者によって証明されていました。その名はアンリ・ポアンカレ。そして、この地球規模の謎を解き明かす鍵は、なんとも奇妙な名前の数学の定理に隠されています。
その名も**「毛玉の定理(Hairy Ball Theorem)」**。
この一見するとユーモラスな名前の定理が、地球の風、そして驚くべきことに、あなたの頭にある「つむじ」の存在理由までをも完璧に説明してしまうのです。この記事では、難解な数式を一切使わずに、日常に潜む謎から宇宙の法則までを繋ぐ、壮大で知的好奇心をくすぐる数学の世界へご案内します。さあ、天才ポアンカレが残した知の冒険に出発しましょう。
第1章:天才アンリ・ポアンカレとは何者か? – 最後の万能科学者
この物語の主役である「毛玉の定理」を理解するためには、まず、それを証明した人物、アンリ・ポアンカレ(Henri Poincaré, 1854-1912)について知る必要があります。彼は単なる数学者ではありません。歴史上「最後の万能科学者」と称されるほどの、規格外の天才でした。
19世紀末から20世紀初頭にかけて活躍したフランスの科学者であるポアンカレは、数学、物理学、天文学、そして哲学の分野で巨大な足跡を残しました。彼の思考の範囲はあまりにも広く、深かったため、同時代人たちは彼の知性に畏敬の念を抱きました。
彼の業績の中でも特に有名なのが、20世紀の数学における最重要未解決問題の一つとされた**「ポアンカレ予想」**です。これは「単連結な3次元閉多様体は3次元球面S³に同相である」という、ほとんどの人にとっては呪文にしか聞こえないような命題ですが、宇宙の形に関する根源的な問いでした。この予想は、彼が提唱してから約100年後の2002年、ロシアの数学者グリゴリー・ペレルマンによってようやく証明され、数学界に大きな衝撃を与えました。
ポアンカレの天才性は、その記憶力にも現れています。彼は一度読んだ本の内容を、ページ数まで含めて完璧に記憶できたと言われています。また、非常に忘れっぽく、極度の近眼であったにもかかわらず、その頭脳は常に宇宙の法則について思索を巡らせていました。
そんな彼が1885年に証明したのが、今回のテーマである「毛玉の定理」です。正式には「偶数次元の球面上には、連続的な非ゼロ接ベクトル場は存在しない」という、これまた暗号のような内容です。しかし、ポアンカレの偉大さは、こうした抽象的な数学の概念が、現実世界の具体的な現象と深く結びついていることを見抜いた点にあります。
彼は、複雑な微分方程式の研究を通じて、力学系の安定性やカオス理論の基礎を築きました。アインシュタインが特殊相対性理論を発表する以前から、ローレンツ変換の持つ群構造を見抜き、相対性理論の数学的な基礎の一部を準備していたとも言われています。
つまり、「毛玉の定理」は、ただの数学的なパズルではありません。物理学や天文学の根源を理解しようとした万能の天才が、世界の構造を記述するために生み出した、強力なツールの一つなのです。次の章では、この天才が生み出した「暗号文」のような定理を、誰にでもわかるように解き明かしていきましょう。
第2章:毛玉はなぜ綺麗にとかせない? – 「毛玉の定理」を体感する
「偶数次元の球面上には、連続的な非ゼロ接ベクトル場は存在しない」
この定理の原文を聞いても、ほとんどの人は思考が停止してしまうでしょう。ご安心ください。ポアンカレの天才的な洞察は、非常に身近で直感的な例え話によって、誰にでも理解することができます。それが、この定理の愛称の由来となった**「毛の生えたボール」**です。
ステップ1:毛の生えたボールを想像する
まず、テニスボールのような球体を思い浮かべてください。そして、その表面全体に、隙間なくびっしりと毛が生えている状態を想像します。一本一本の毛は、まっすぐにボールの表面から垂直に生えているのではなく、表面に沿って寝ている状態です。
ステップ2:「とかす」という行為を考える
次に、この毛の生えたボールを、小さな櫛(くし)を使って綺麗に「とかす」ことを考えてみましょう。「綺麗にとかす」とは、全ての毛を滑らかに、一方向に流れるように整えることです。隣り合う毛が急に逆方向を向いたり、絡まったりすることなく、全体としてスムーズな毛の流れを作ることを目指します。
ステップ3:必ず現れる「問題点」
さあ、ボールのどこか一点から櫛を入れ、毛をとかし始めてください。最初は順調に進むでしょう。ある部分の毛は、綺麗に同じ方向を向いて流れていきます。しかし、ボール全体をくまなく、完璧に滑らかにとかし終えようとすると、必ず、どうしても上手くいかない点が出てきてしまうのです。
具体的には、以下のどちらかの「問題点」が必ず現れます。
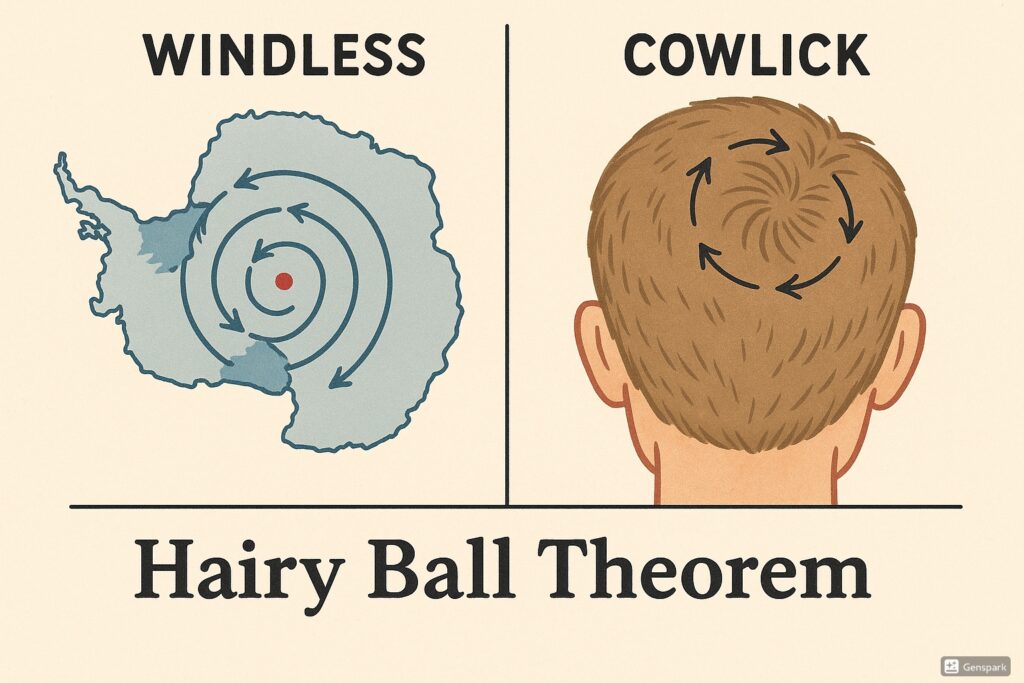
- つむじ(渦巻き): ある一点を中心に、毛が渦を巻くように集まってしまう場所。この中心点では、毛の向きを定めることができません。
- 逆立ち(カウリック): ある一点で、毛がボールの表面から垂直にピョンと立ち上がってしまう場所。これも「表面に沿って寝かせる」というルールを破ってしまいます。
<center>(画像:毛の生えたボールにつむじができているイラスト)</center>
いくら頑張っても、どんなに器用な人が挑戦しても、この「つむじ」か「逆立ち」をボール上から完全に消し去ることは不可能なのです。ボール全体に滑らかな毛の流れを作ろうとすればするほど、その流れの歪みはどこか一点に集中し、特異点として現れてしまいます。
数学的な翻訳
この直感的な現象を、数学の言葉に翻訳してみましょう。
- ボールの表面(球面):これは数学的な「2次元球面」です。私たちの住む3次元空間に浮かぶボールの表面は、2次元の広がりしか持っていません(私たちはボールの表面を前後左右には動けますが、上下(内部や外部)には動けないため)。「2」は偶数なので、定理の「偶数次元の球面」という条件に当てはまります。
- 毛の向きと長さ:これは「ベクトル」に対応します。ベクトルとは、向きと大きさ(この場合は毛の長さ)を持つ矢印のことです。毛をとかすという行為は、ボールの表面上の各点に、滑らかに変化するベクトル(矢印)を割り当てる作業(ベクトル場を作る)に他なりません。
- 「綺麗にとかす」:これは「連続的なベクトル場」を作ることを意味します。つまり、隣り合う点では、ベクトルの向きも急に変わらず、滑らかに繋がっている状態です。
- 「毛が逆立たない・渦を巻かない」:これは、全てのベクトルがゼロではない(長さが0ではない)状態、つまり「非ゼロ」であることを意味します。つむじの中心や毛が逆立つ根本は、どちらを向けばいいかわからない、いわば「向きの定義できない点」であり、数学的には「ベクトルがゼロになる点」として扱われます。
これらを繋ぎ合わせると、「毛玉の定理」の主張が明確になります。
「(2次元の)球面上に、毛(ベクトル)を割り当てようとしても、必ずどこか一箇所は、毛の向きが定義できない点(ベクトルがゼロになる点)が存在する」
つまり、毛の生えたボールを綺麗にとかしきれないのは、私たちの不器用さが原因なのではなく、宇宙の法則、数学的な摂理がそれを許さないからなのです。
第3章:あなたの「つむじ」は宇宙の法則の証明だった
さて、毛の生えたボールの例えで、「つむじ」という言葉が出てきました。ここで、鏡の前に立って、ご自身の頭をよく観察してみてください。多くの人の頭頂部や後頭部には、髪の毛が渦を巻いている中心点、すなわち「つむじ」があるはずです。
実は、このあなたの「つむじ」こそが、「毛玉の定理」が私たちの身体に現れた、最も身近で完璧な証明なのです。
考えてみてください。
- 私たちの頭:多少の凹凸はありますが、おおよそ「球体」と見なすことができます。
- 髪の毛:頭皮という「球面」に生えた「毛」です。そして、それぞれの毛は、頭皮に沿って特定の方向を向いています。これはまさに、頭という球面上に描かれた「ベクトル場」です。
もし「毛玉の定理」が間違っているならば、私たちは髪の毛を、つむじを作ることなく、頭のてっぺんからつま先まで、完全に滑らかな一方向の流れとして生やすことができたはずです。しかし、現実はそうではありません。私たちの髪の毛は、頭という球面上に生えているがゆえに、定理の制約から逃れることができず、必ずどこかに流れの破綻点、つまり「つむじ」を生み出さざるを得ないのです。
つむじは、髪の流れが渦を巻く中心であり、その一点においては髪の毛の「向き」が定まりません。これこそが、毛玉の定理が予言する「ベクトルがゼロになる点」そのものです。
「でも、つむじが2つある人もいるし、中にはつむじが見当たらない人もいるじゃないか?」
良い質問です。これもまた、「毛玉の定理」の奥深さを示しています。
- つむじが複数ある場合:定理が保証するのは、「少なくとも1つの特異点(つむじ)が存在する」ということです。2つあっても、3つあっても、定理とは矛盾しません。実際、渦の向きが違うつむじが複数存在することで、全体の髪の流れのバランスを取っていると考えることもできます。
- つむじが見当たらない場合:一見つむじがないように見える人でも、髪の流れを詳細に観察すると、どこかに流れが合流する「分け目」のようなラインや、流れが分岐する点が存在します。これらも広義の特異点であり、滑らかなベクトル場の連続性が破綻している点と解釈できます。完全に滑らかな流れは、やはり球面上には実現不可能なのです。
私たちは、生まれながらにして、自分の身体に深遠な数学的真理の証を刻み込んでいます。あなたが毎朝、鏡の前で格闘している寝癖や、言うことを聞かないつむじは、単なる遺伝やクセではなく、ポアンカレが発見した宇宙の法則の現れだったのです。そう考えると、少しだけ自分のつむじが愛おしく思えてきませんか?
第4章:地球を巨大な「毛玉」と見なす – 無風地点の謎を解く
いよいよ、この物語の核心に迫ります。私たちの小さな「つむじ」の謎を解いた「毛玉の定理」を、今度は壮大なスケール、すなわち地球全体に適用してみましょう。
- 地球:言わずと知れた、ほぼ完璧な「球体」です。
- 地球上の風:地球の表面(地表や上空)を吹く風は、各地点で「風速」と「風向」を持っています。これはまさしく、向きと大きさを持つ「ベクトル」です。地球全体を覆う大気の流れは、地球という球面上に広がる巨大な「ベクトル場」と見なすことができます。
ここで、「毛玉の定理」を思い出してください。
「球面上には、連続的な非ゼロ接ベクトル場は存在しない」
この定理を、地球と風のシステムに当てはめて翻訳すると、次のようになります。
「地球という球面上に広がる風の流れ(ベクトル場)には、必ずどこか一箇所、風のベクトルがゼロになる点が存在しなければならない」
ベクトルがゼロになるとはどういうことか?それは、風の「向き」が定まらず、そして「大きさ(風速)」がゼロであることを意味します。つまり、**「無風地点」**です。
これは、驚くべき結論です。地球上のどこかで巨大なハリケーンが発生し、猛烈な嵐が吹き荒れていても、あるいは偏西風が強く吹いていても、それら全ての風の流れを考慮した上で、地球上のどこか一点では、必ず風がピタリと止まっている場所が存在する。それが数学的に保証されているのです。
これは、天気予報で偶然観測される「無風」とは次元の違う話です。ある都市の風速がたまたま0m/sになることはあっても、それは局所的な現象です。しかし「毛玉の定理」が保証するのは、地球全体を一つのシステムとして見たときに、構造的に「無風点」が存在せざるを得ない、という数学的な必然性なのです。
では、その「無風地点」とは、具体的にどこにあるのでしょうか?
その最もわかりやすい例が、高気圧の中心や低気圧の中心です。
- 高気圧:中心から外側に向かって、時計回りに風が吹き出しています。その中心点では、風はどちらの方向にも吹き出しておらず、穏やかな下降気流があるのみで、水平方向の風速はほぼゼロになります。
- 低気圧(台風など):外側から中心に向かって、反時計回りに風が渦を巻いて吹き込んでいます。そして、その中心には「台風の目」と呼ばれる、風が非常に弱く穏やかな領域が存在します。
これらの気圧の中心は、まさに地球という毛玉にできた「つむじ」に他なりません。風というベクトル場が、地球という球面上に存在するために、必然的に生まれてしまった特異点なのです。もちろん、現実の気象はもっと複雑で、無風地点は常に移動し、生成と消滅を繰り返しています。しかし、どの瞬間を切り取っても、地球上のどこかに必ずそうした点が存在する、というのが「毛玉の定理」の力強い予言なのです。
私たちは、日々の天気図の中に、100年以上前にポアンカレが証明した数学的真理の現れを、毎日目にしているというわけです。
第5章:コーヒーカップから宇宙まで – 「毛玉の定理」の意外な応用
「毛玉の定理」は、つむじや地球の風を説明するだけの、面白い豆知識で終わるものではありません。この定理は、一見すると無関係に見える様々な科学技術の分野で、基礎的な原理として重要な役割を果たしています。
1. コンピュータグラフィックス(CG)
映画やゲームでリアルな3Dキャラクターや惑星を作る際、球体オブジェクトにテクスチャ(模様や質感の画像)を滑らかに貼り付ける作業は非常に重要です。しかし、ここで「毛玉の定理」が壁として立ちはだかります。
球体にテクスチャを貼り付けようとすると、北極や南極のような「極」にあたる部分で、どうしても画像が歪んだり、一点に収束してしまったりする問題が起こります。これは、球面上に歪みのない座標(ベクトル場)を連続的に設定することが不可能である、という「毛玉の定理」の現れです。CGアーティストたちは、この数学的な制約を理解した上で、歪みが目立たないようにテクスチャの貼り方を工夫するなどのテクニックを駆使しています。
2. ロボット工学
球体の表面を移動するロボットや、全方位カメラの制御などを考える際にも、この定理は重要になります。例えば、球体ロボットに「常に前方を向きながら、滑らかに移動せよ」という命令を与えようとしても、ある特定の点(特異点)では、どちらが「前方」なのかを定義できなくなり、制御が破綻する可能性があります。この特異点の存在をあらかじめ計算に入れておくことで、より安定したロボットの制御システムを設計することができるのです。
3. 経済学と不動点定理
「毛玉の定理」は、より一般的には「不動点定理」という数学の一分野に関連しています。不動点定理とは、「ある種の操作を行ったときに、動かない点(不動点)が必ず存在する」ことを保証する定理群のことです。
これは経済学において、市場の「均衡価格」が存在することを証明するためなどに使われます。需要と供給という、市場を動かす様々なベクトル(力)が働いている中で、全ての力が釣り合って価格が安定する「不動点(均衡点)」が、特定の条件下で必ず存在することを示すことができるのです。複雑な社会現象の中に潜む安定点を見つけ出すための、強力な理論的支柱となっています。
ドーナツ型なら可能?
ちなみに、「毛玉の定理」が適用されるのは「穴のない」球体(専門用語では種数0の曲面)です。もし、穴が一つ空いたドーナツの形(トーラス)であれば、全ての毛を綺麗に同じ方向にとかすことが可能です。ドーナツの表面に沿って、穴をぐるりと回るように、滑らかな毛の流れを作ることができるのです。この事実は、物体の「形(トポロジー)」が、その上で起こる現象の可能性を根本的に決定づけていることを示しており、現代数学の重要なテーマの一つとなっています。
コーヒーカップの取っ手(ドーナツ型)の表面と、ボール(球体)の表面では、許される物理法則が違う、と考えると、数学の奥深さが感じられるのではないでしょうか。
結論:日常に隠された数学の美しさ
私たちは、フランスの天才数学者アンリ・ポアンカ레が証明した「毛玉の定理」を巡る旅をしてきました。
それは、毛の生えたボールは綺麗にとかせない、という素朴な疑問から始まりました。
そして、その答えが、私たちの頭にある「つむじ」の存在理由を説明し、さらには、地球上に常に「無風地点」が存在する驚くべき事実を解き明かしてくれました。
最後には、CGやロボット工学といった最先端技術にも、その原理が深く関わっていることを見てきました。
一つの数学の定理が、これほどまでに広範囲で、スケールの違う現象を、同じ一つの論理で貫いている。これこそが、数学という学問の持つ力であり、美しさです。
次にあなたが天気図で高気圧や低気圧の渦を見たとき、あるいは鏡の前でつむじと格闘するとき、ぜひ思い出してください。あなたは今、宇宙の根本的な構造、数学的な必然性と対峙しているのだと。
私たちの世界は、一見すると複雑で無秩序に見えるかもしれません。しかし、その背後には、ポアンカレのような天才たちが見つけ出した、シンプルで揺るぎない法則が隠されています。日常に潜む「なぜ?」に目を向けるとき、世界はもっと面白く、もっと知的な驚きに満ちたものになるのです。